Is het je wel eens opgevallen dat de spiegeling van een object een andere vorm heeft en andere dimensies heeft dan het eigenlijke object?
Dit is iets dat niet snel opvalt, vooral niet bij natuurlijke objecten zoals bomen. Die staan immers schots en scheef en de takken steken alle kanten op. Maar bij de spiegeling van een flatgebouw is dit duidelijker zichtbaar. Eén en ander heeft te maken met het natuurkundige begrip: hoek van inval – hoek van uitval. Ik heb geprobeerd dit in het volgende tekeningetje weer te geven.
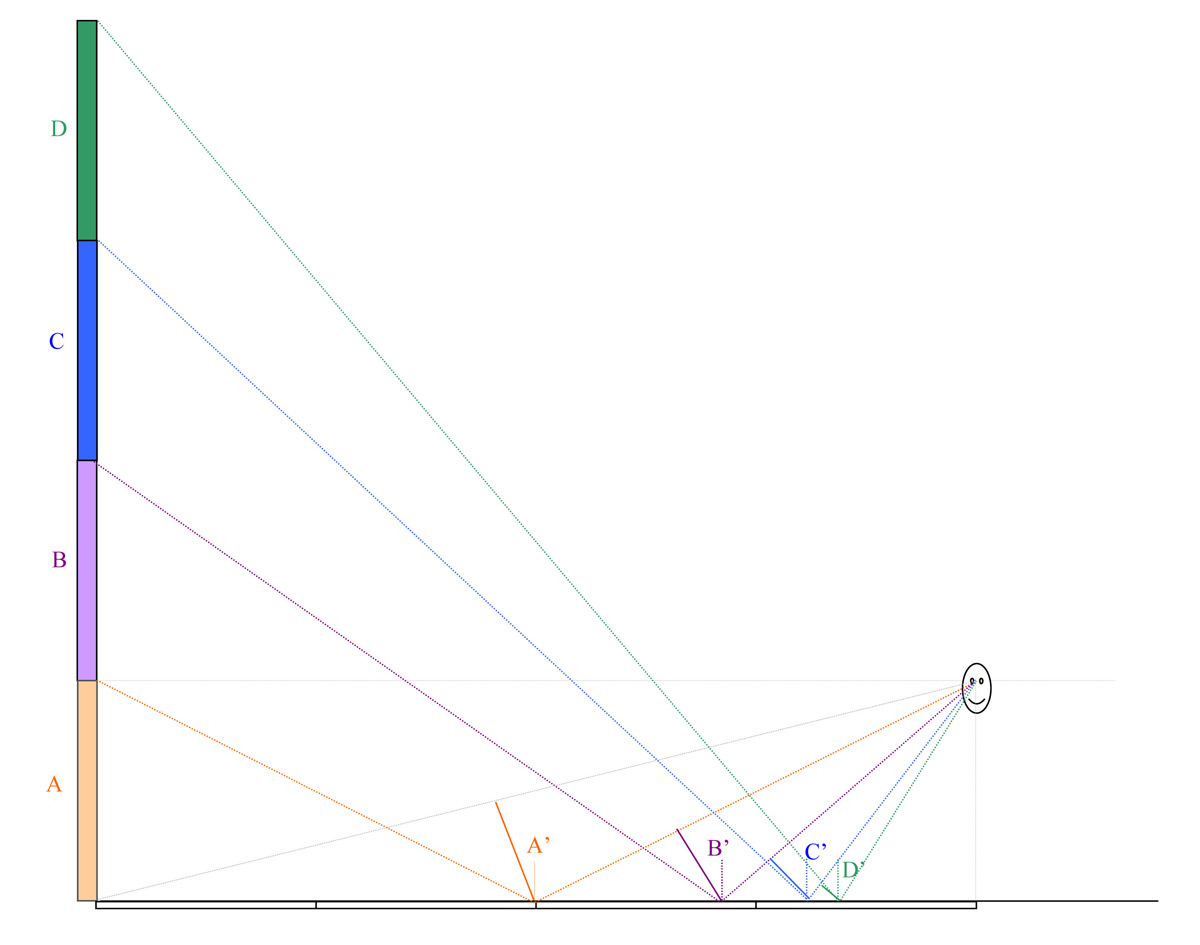
De waarnemer staat aan de waterkant en kijkt naar een flatgebouw aan de overzijde. Iedere verdieping is qua hoogte identiek. Dit is weergegeven met de codering: A, B, C, D. De waarnemer ziet de weerspiegelde afbeelding weergegeven met de aanduiding: A’, B’, C’, D’.
Immers: Stel je voor, het flatgebouw is 100 meter hoog, dan ziet de waarnemer nog steeds de reflectie van de bovenste verdieping. Maar wel als een heel smal vlakje, geprojecteerd op het water vlak voor zijn voeten.
Moet je met schilderen rekening houden met een dergelijk natuurkundig aspect? Zoals bij het schilderen van de weerspiegeling van een wolkenlucht in het natte noordzeestrand? Het belangrijkste is dat je leert om dit te zien. Werk verder op je gevoel.
De weerspiegelingen van de bomen in het water zijn veel groter dan de bomen zelf.